Z-transform
From Wikipedia, the free encyclopedia
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation.It can be considered as a discrete-time equivalent of the Laplace transform. This similarity is explored in the theory of time scale calculus.
History
The basic idea now known as the Z-transform was known to Laplace, and re-introduced in 1947 by W. Hurewicz as a tractable way to solve linear, constant-coefficient difference equations.[1] It was later dubbed "the z-transform" by Ragazzini and Zadeh in the sampled-data control group at Columbia University in 1952.[2][3]The modified or advanced Z-transform was later developed and popularized by E. I. Jury.[4][5]
The idea contained within the Z-transform is also known in mathematical literature as the method of generating functions which can be traced back as early as 1730 when it was introduced by de Moivre in conjunction with probability theory.[6] From a mathematical view the Z-transform can also be viewed as a Laurent series where one views the sequence of numbers under consideration as the (Laurent) expansion of an analytic function.
Definition
The Z-transform, like many integral transforms, can be defined as either a one-sided or two-sided transform.Bilateral Z-transform
The bilateral or two-sided Z-transform of a discrete-time signal x[n] is the formal power series X(z) defined as is the complex argument (also referred to as angle or phase) in radians.
is the complex argument (also referred to as angle or phase) in radians.Unilateral Z-transform
Alternatively, in cases where x[n] is defined only for n ≥ 0, the single-sided or unilateral Z-transform is defined asAn important example of the unilateral Z-transform is the probability-generating function, where the component
![x[n]](http://upload.wikimedia.org/wikipedia/en/math/d/3/b/d3baaa3204e2a03ef9528a7d631a4806.png) is the probability that a discrete random variable takes the value
is the probability that a discrete random variable takes the value  , and the function
, and the function  is usually written as
is usually written as  , in terms of
, in terms of  . The properties of Z-transforms (below) have useful interpretations in the context of probability theory.
. The properties of Z-transforms (below) have useful interpretations in the context of probability theory.Geophysical definition
In geophysics, the usual definition for the Z-transform is a power series in z as opposed to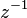 . This convention is used by Robinson and Treitel and by Kanasewich.[citation needed] The geophysical definition is
. This convention is used by Robinson and Treitel and by Kanasewich.[citation needed] The geophysical definition isInverse Z-transform
The inverse Z-transform is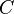 is a counterclockwise closed path encircling the origin and entirely in the region of convergence (ROC). In the case where the ROC is causal (see Example 2), this means the path
is a counterclockwise closed path encircling the origin and entirely in the region of convergence (ROC). In the case where the ROC is causal (see Example 2), this means the path 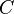 must encircle all of the poles of
must encircle all of the poles of 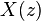 .
.A special case of this contour integral occurs when
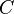 is the unit circle (and can be used when the ROC includes the unit circle which is always guaranteed when
is the unit circle (and can be used when the ROC includes the unit circle which is always guaranteed when 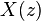 is stable, i.e. all the poles are within the unit circle). The inverse Z-transform simplifies to the inverse discrete-time Fourier transform:
is stable, i.e. all the poles are within the unit circle). The inverse Z-transform simplifies to the inverse discrete-time Fourier transform:Region of convergence
The region of convergence (ROC) is the set of points in the complex plane for which the Z-transform summation converges.Example 1 (no ROC)
Let![x[n] = 0.5^n\](http://upload.wikimedia.org/wikipedia/en/math/a/e/3/ae38b507e5e88ead1c7b0e035cde9046.png) . Expanding
. Expanding ![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) on the interval
on the interval 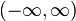 it becomes
it becomes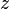 that satisfy this condition.
that satisfy this condition.Example 2 (causal ROC)
![x[n] = 0.5^n u[n]\](http://upload.wikimedia.org/wikipedia/en/math/5/7/6/57674052f63a5b5b55d69d0b097e5695.png) (where
(where  is the Heaviside step function). Expanding
is the Heaviside step function). Expanding ![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) on the interval
on the interval 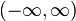 it becomes
it becomes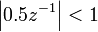 which can be rewritten in terms of
which can be rewritten in terms of 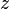 as
as 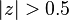 . Thus, the ROC is
. Thus, the ROC is 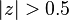 . In this case the ROC is the complex plane with a disc of radius 0.5 at the origin "punched out".
. In this case the ROC is the complex plane with a disc of radius 0.5 at the origin "punched out".Example 3 (anticausal ROC)
![x[n] = -(0.5)^n u[-n-1]\](http://upload.wikimedia.org/wikipedia/en/math/9/5/0/9508c0a3dd6fab9c51bd316852844bf1.png) (where
(where  is the Heaviside step function). Expanding
is the Heaviside step function). Expanding ![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) on the interval
on the interval 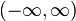 it becomes
it becomes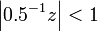 which can be rewritten in terms of
which can be rewritten in terms of 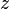 as
as 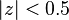 . Thus, the ROC is
. Thus, the ROC is 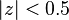 . In this case the ROC is a disc centered at the origin and of radius 0.5.
. In this case the ROC is a disc centered at the origin and of radius 0.5.What differentiates this example from the previous example is only the ROC. This is intentional to demonstrate that the transform result alone is insufficient.
Examples conclusion
Examples 2 & 3 clearly show that the Z-transform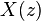 of
of ![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) is unique when and only when specifying the ROC. Creating the pole-zero plot
for the causal and anticausal case show that the ROC for either case
does not include the pole that is at 0.5. This extends to cases with
multiple poles: the ROC will never contain poles.
is unique when and only when specifying the ROC. Creating the pole-zero plot
for the causal and anticausal case show that the ROC for either case
does not include the pole that is at 0.5. This extends to cases with
multiple poles: the ROC will never contain poles.In example 2, the causal system yields an ROC that includes
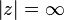 while the anticausal system in example 3 yields an ROC that includes
while the anticausal system in example 3 yields an ROC that includes 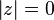 .
.In systems with multiple poles it is possible to have an ROC that includes neither
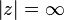 nor
nor 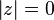 . The ROC creates a circular band. For example,
. The ROC creates a circular band. For example, ![x[n] = 0.5^nu[n] - 0.75^nu[-n-1]\](http://upload.wikimedia.org/wikipedia/en/math/5/b/b/5bb87341b337d0d121453a4b16d01d31.png) has poles at 0.5 and 0.75. The ROC will be
has poles at 0.5 and 0.75. The ROC will be 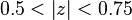 , which includes neither the origin nor infinity. Such a system is called a mixed-causality system as it contains a causal term
, which includes neither the origin nor infinity. Such a system is called a mixed-causality system as it contains a causal term ![0.5^nu[n]\](http://upload.wikimedia.org/wikipedia/en/math/3/1/3/3133def49d00cf59a1e73e28b6988e9c.png) and an anticausal term
and an anticausal term ![-(0.75)^nu[-n-1]\](http://upload.wikimedia.org/wikipedia/en/math/6/c/3/6c39198fd187e5e3a8b2993efc0afceb.png) .
.The stability of a system can also be determined by knowing the ROC alone. If the ROC contains the unit circle (i.e.,
 ) then the system is stable. In the above systems the causal system (Example 2) is stable because
) then the system is stable. In the above systems the causal system (Example 2) is stable because 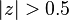 contains the unit circle.
contains the unit circle.If you are provided a Z-transform of a system without an ROC (i.e., an ambiguous
![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) ) you can determine a unique
) you can determine a unique ![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) provided you desire the following:
provided you desire the following:- Stability
- Causality
The unique
![x[n]\](http://upload.wikimedia.org/wikipedia/en/math/c/1/4/c1466b9927640af95f78274058d272d9.png) can then be found.
can then be found.
![X(z) = \mathcal{Z}\{x[n]\} = \sum_{n=-\infty}^{\infty} x[n] z^{-n}](http://upload.wikimedia.org/wikipedia/en/math/4/7/9/4799f830eb930ecb74fe5368df6d7ab6.png)
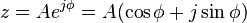
![X(z) = \mathcal{Z}\{x[n]\} = \sum_{n=0}^{\infty} x[n] z^{-n}. \](http://upload.wikimedia.org/wikipedia/en/math/e/3/4/e342b69a450fef8889304628209e08c3.png)
![X(z) = \mathcal{Z}\{x[n]\} = \sum_{n} x[n] z^{n}. \](http://upload.wikimedia.org/wikipedia/en/math/7/a/d/7adafd11922f7dc708923f753a1b470b.png)
![x[n] = \mathcal{Z}^{-1} \{X(z) \}= \frac{1}{2 \pi j} \oint_{C} X(z) z^{n-1} dz \](http://upload.wikimedia.org/wikipedia/en/math/0/6/6/06691f5e61f96167aed6ab2d28fa4363.png)
![x[n] = \frac{1}{2 \pi} \int_{-\pi}^{+\pi} X(e^{j \omega}) e^{j \omega n} d \omega. \](http://upload.wikimedia.org/wikipedia/en/math/0/8/3/0835788bfa1380f6c0bc606f2da0a921.png)
![ROC = \left\{ z : \left|\sum_{n=-\infty}^{\infty}x[n]z^{-n}\right| < \infty \right\}](http://upload.wikimedia.org/wikipedia/en/math/9/6/c/96caf8885ff1d0531bed5670622fc90a.png)
![x[n] = \{..., 0.5^{-3}, 0.5^{-2}, 0.5^{-1}, 1, 0.5, 0.5^2, 0.5^3, ...\} = \{..., 2^3, 2^2, 2, 1, 0.5, 0.5^2, 0.5^3, ...\}\ .](http://upload.wikimedia.org/wikipedia/en/math/1/e/5/1e5620a51449d4620bcde1523cfdf689.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} \rightarrow \infty\ .](http://upload.wikimedia.org/wikipedia/en/math/9/1/b/91b45b00cb7129c677014ab6f52c3753.png)

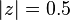 is shown as a dashed black circle
is shown as a dashed black circle![x[n] = \{..., 0, 0, 0, 1, 0.5, 0.5^2, 0.5^3, ...\}.\](http://upload.wikimedia.org/wikipedia/en/math/8/7/b/87b3f8c3d6429d893a4e6022247cd16a.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} = \sum_{n=0}^{\infty}0.5^nz^{-n} = \sum_{n=0}^{\infty}\left(\frac{0.5}{z}\right)^n = \frac{1}{1 - 0.5z^{-1}}.\](http://upload.wikimedia.org/wikipedia/en/math/2/1/c/21cdd138c51cbb6f6456cc9f15489c29.png)
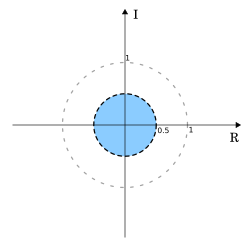
![x[n] = \{..., -(0.5)^{-3}, -(0.5)^{-2}, -(0.5)^{-1}, 0, 0, 0, 0, ...\}.\](http://upload.wikimedia.org/wikipedia/en/math/8/7/9/87908bb58989914865eebbc1776aa508.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} = -\sum_{n=-\infty}^{-1}0.5^nz^{-n} = -\sum_{n=-\infty}^{-1}\left(\frac{z}{0.5}\right)^{-n}\](http://upload.wikimedia.org/wikipedia/en/math/1/e/6/1e6a35a12a88d07372c071a528f1b5d1.png)
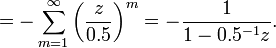

Z-transform comes in mathematics and signal processing, the Z-transform converts a sequence of real or complex numbers into a complex frequency-domain representation.It can be considered as a discrete-time equivalent of the Laplace transform.
ReplyDeleteCritical Point
Thanks
Delete