In
control theory, the
state-transition matrix is a matrix whose product with the state vector

at an initial time

gives

at a later time

. The state-transition matrix can be used to obtain the general solution of linear dynamical systems. It is also known as the
matrix exponential.
Overview
Consider the general linear
state space model
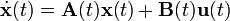
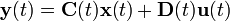
The general solution is given by

The state-transition matrix
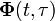
, given by

where
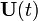
is the fundamental solution matrix that satisfies
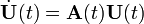
is a
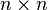
matrix that is a linear mapping onto itself, i.e., with
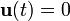
, given the state
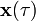
at any time

, the state at any other time

is given by the mapping

While the state transition matrix φ is not completely unknown, it must always satisfy the following relationships:
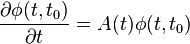 and
and
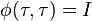 for all
for all  and where
and where 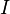 is the identity matrix.[1]
is the identity matrix.[1]
And φ also must have the following properties:
-
If the system is
time-invariant, we can define φ as:
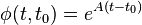
 at an initial time
at an initial time  gives
gives  at a later time
at a later time  . The state-transition matrix can be used to obtain the general solution of linear dynamical systems. It is also known as the matrix exponential.
. The state-transition matrix can be used to obtain the general solution of linear dynamical systems. It is also known as the matrix exponential.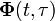 , given by
, given by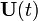 is the fundamental solution matrix that satisfies
is the fundamental solution matrix that satisfies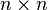 matrix that is a linear mapping onto itself, i.e., with
matrix that is a linear mapping onto itself, i.e., with 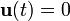 , given the state
, given the state 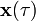 at any time
at any time  , the state at any other time
, the state at any other time  is given by the mapping
is given by the mapping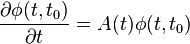 and
and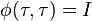 for all
for all  and where
and where 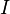 is the identity matrix.[1]
is the identity matrix.[1]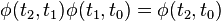

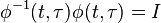
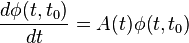
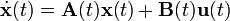
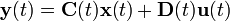


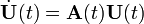

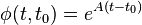
No comments:
Post a Comment