Programming + Errors: laplace of state space model

Wednesday, May 16, 2012

laplace of state space model

Transfer function

The "transfer function" of a continuous time-invariant linear state-space model can be derived in the following way:
First, taking the Laplace transform of

$\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)$

yields

$s\mathbf{X}(s) = A \mathbf{X}(s) + B \mathbf{U}(s). \,$

Next, we simplify for $\mathbf{X}(s)$ , giving

$(s\mathbf{I} - A)\mathbf{X}(s) = B\mathbf{U}(s), \,$

and thus

$\mathbf{X}(s) = (s\mathbf{I} - A)^{-1}B\mathbf{U}(s). \,$

Substituting for $\mathbf{X}(s)$ in the output equation

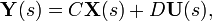$\mathbf{Y}(s) = C\mathbf{X}(s) + D\mathbf{U}(s),$ giving

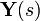$\mathbf{Y}(s) = C((s\mathbf{I} - A)^{-1}B\mathbf{U}(s)) + D\mathbf{U}(s). \,$

Because the transfer function $\mathbf{G}(s)$ is defined as the ratio of the output to the input of a system, we take

$\mathbf{G}(s) = \mathbf{Y}(s) / \mathbf{U}(s)$

and substitute the previous expression for $\mathbf{Y}(s)$ with respect to 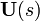$\mathbf{U}(s)$ , giving

$\mathbf{G}(s) = C(s\mathbf{I} - A)^{-1}B + D. \,$

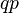Clearly $\mathbf{G}(s)$ must have $q$ by $p$ dimensionality, and thus has a total of $qp$ elements. So for every input there are $q$ transfer functions with one for each output. This is why the state-space representation can easily be the preferred choice for multiple-input, multiple-output (MIMO) system

Programming + Errors

Wednesday, May 16, 2012

laplace of state space model

Transfer function

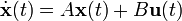
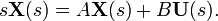
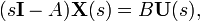
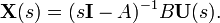
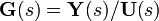
No comments:

Post a Comment

Blog Archive